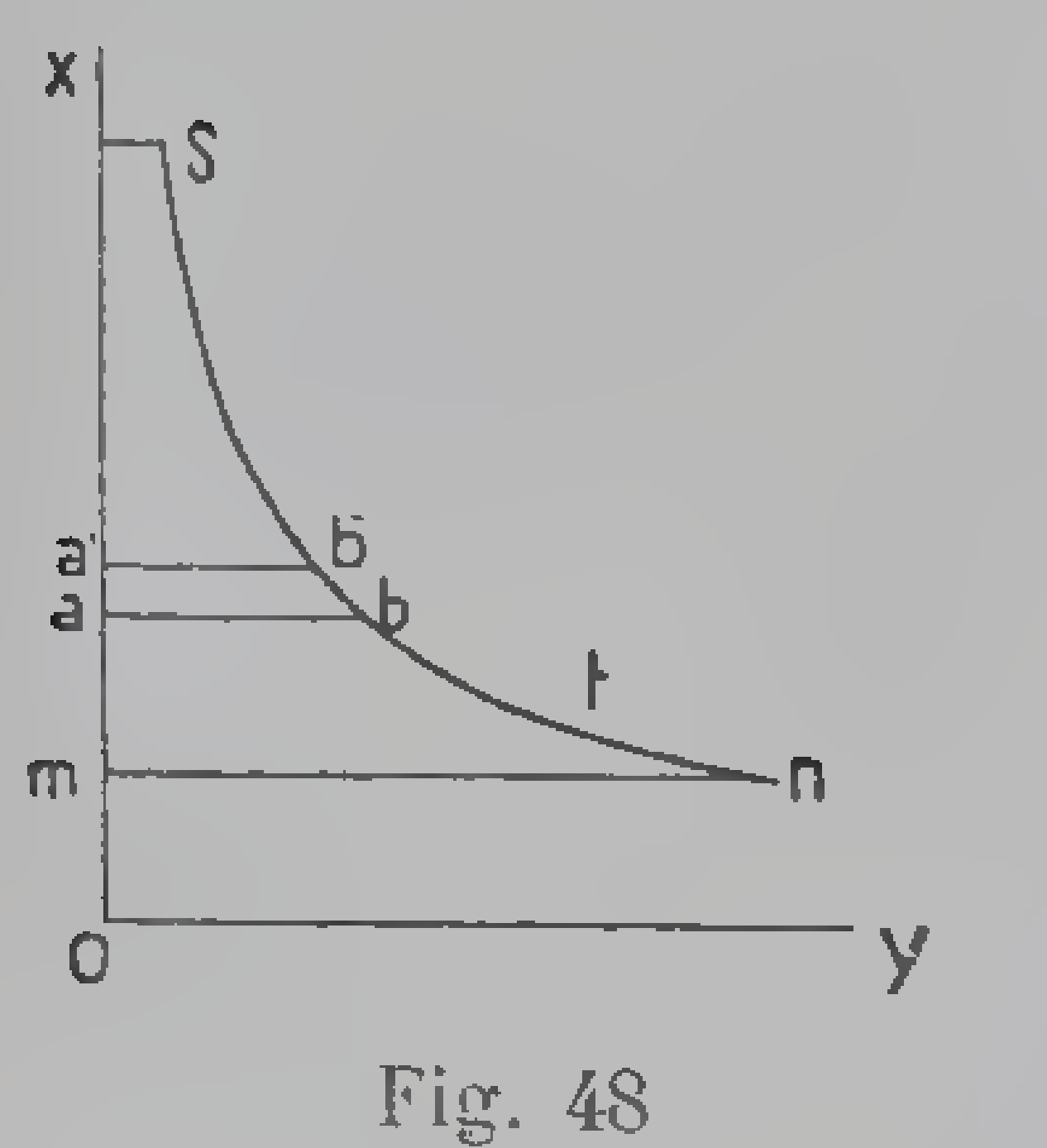
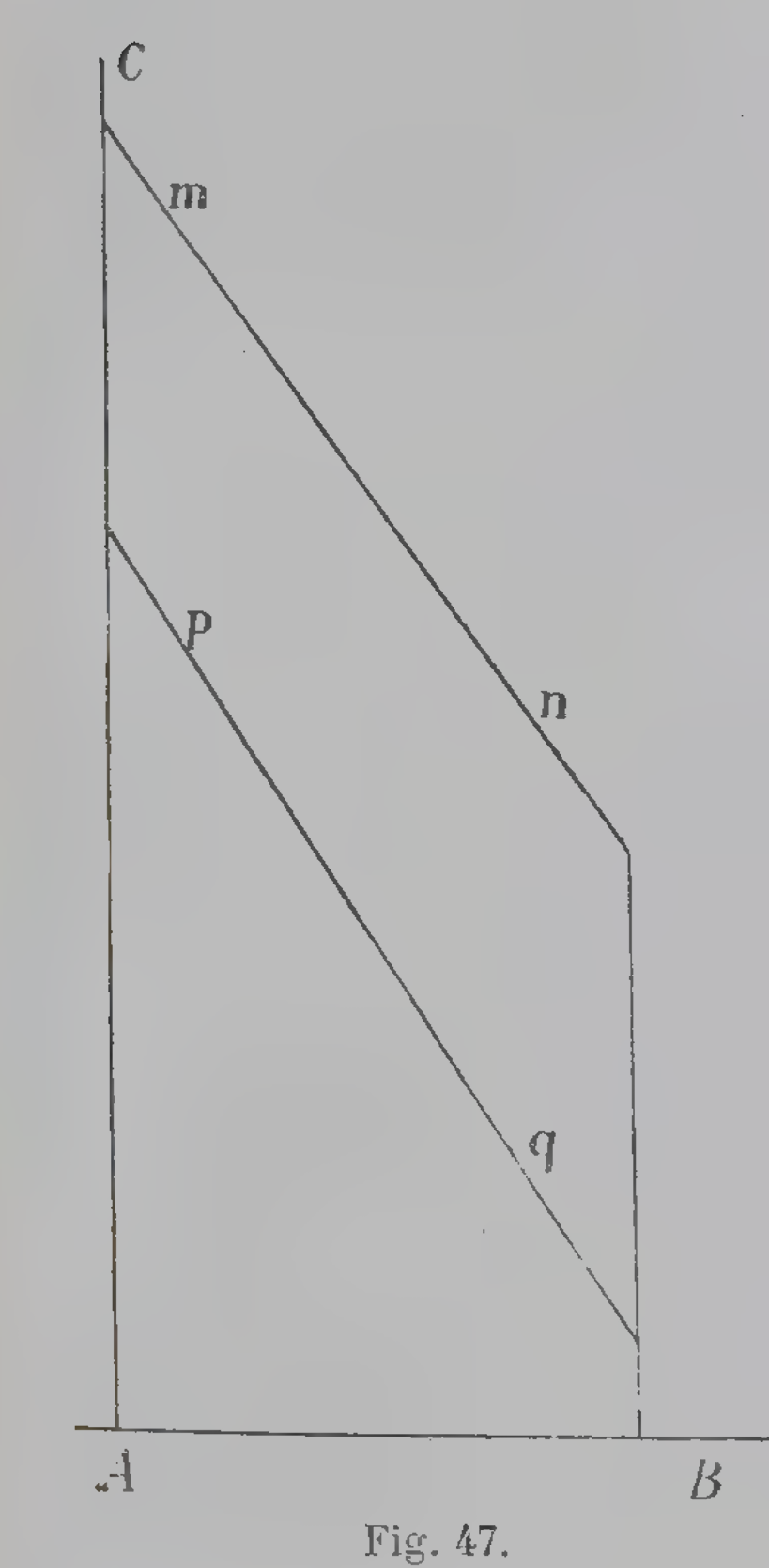
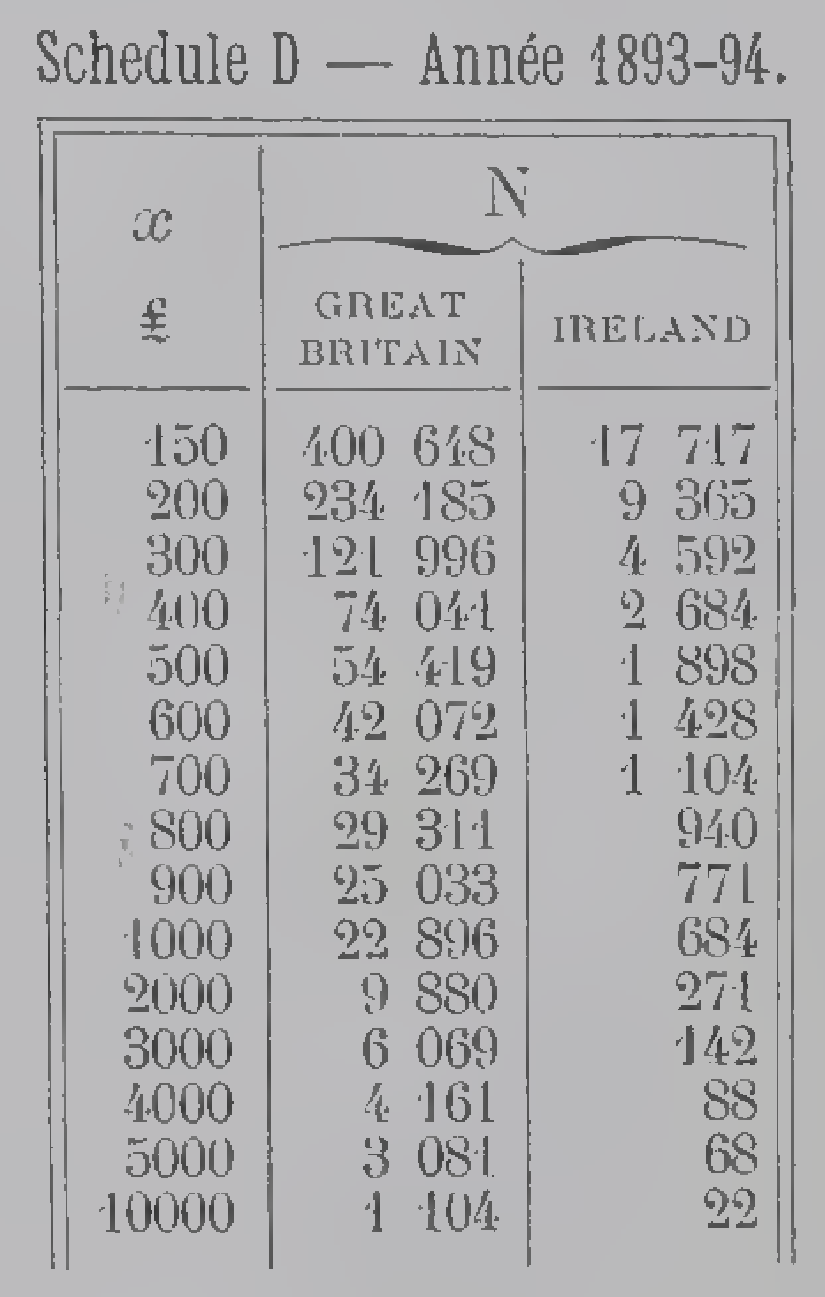
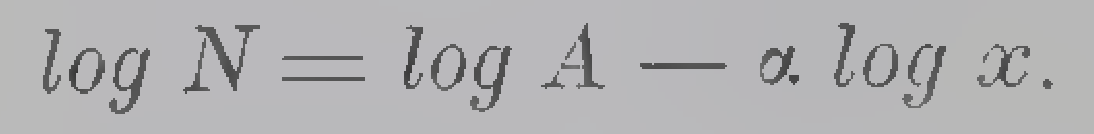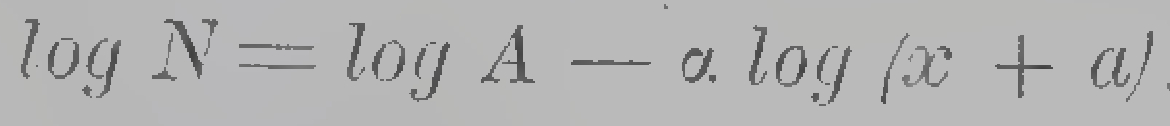# Import normal distribution method
from scipy.stats import norm
mean, var, skew, kurt = norm.stats(moments='mvsk')
fig, axs = plt.subplots(2, 2, sharey=True, figsize=(7,6))
fig.suptitle("Pareto Distribution vs. Normal Distribution", color = "r")
# Plot upper left: PDF Pareto
axs[0,0].set_xlim(left=0, right=(x_max/2))
axs[0,0].grid(visible=True, which='both', axis='both', color='darkgrey', linestyle='-', linewidth=0.25)
plt.xticks(np.arange(0, ((x_max/2)+1), step=1), fontsize = 10) # Set label locations.
axs[0,0].set_title("PDF: Pareto", color = "b")
# Function
x=np.linspace(x_min, (x_max/2) , num=1000)
y = pareto_PDF (x, alpha)
axs[0,0].plot(x, y, 'b-', lw=2, alpha=1, label='pareto pdf')
# Plot upper right: PDF Normal
axs[0,1].set_xlim(left=-3, right=3)
axs[0,1].grid(visible=True, which='both', axis='both', color='darkgrey', linestyle='-', linewidth=0.25)
plt.xticks(np.arange(-3*var, 3*var, step=var), fontsize = 10) # Set label locations.
axs[0,1].set_title("PDF: Normal", color = "g")
# Function
x = np.linspace(norm.ppf(0.01), norm.ppf(0.99), 100)
axs[0,1].plot(x, norm.pdf(x), 'g-', lw=2, alpha=1, label='norm pdf')
#Plot lower left: CDF Pareto
axs[1,0].set_xlim(left=0, right=x_max/2)
axs[1,0].grid(visible=True, which='both', axis='both', color='darkgrey', linestyle='-', linewidth=0.25)
plt.xticks(np.arange(0, ((x_max/2)+1), step=1), fontsize = 10) # Set label locations.
axs[1,0].set_title("CDF: Pareto", color = "b")
# Function
x=np.linspace(x_min, (x_max/2) , num=1000)
y = pareto_CDF (x, alpha)
axs[1,0].plot(x, y, 'b-', lw=2, alpha=1, label='norm pdf')
#Plot lower right: CDF Normal
axs[1,1].set_xlim(left=-3, right=3)
axs[1,1].set_ylim(bottom=0, top=1.05)
axs[1,1].grid(visible=True, which='both', axis='both', color='darkgrey', linestyle='-', linewidth=0.25)
plt.xticks(np.arange(-3*var, 3*var, step=var), fontsize = 10) # Set label locations.
axs[1,1].set_title("CDF: Normal", color = "g")
# Function
x = np.linspace(norm.ppf(0.01), norm.ppf(0.99), 1000)
axs[1,1].plot(x, norm.cdf(x), 'g-', lw=2, alpha=1, label='norm pdf')
for ax in axs.flat:
ax.set(xlabel=None, ylabel=None)
ax.set(yticklabels=[])
ax.set(xticklabels=[])
plt.show()